How Geometry is Fundamental for Chess

Understanding Geometrical Concepts

Humans are the only animals that we know that understand geometrical concepts.

Humans are the only animals that we know that understand geometrical concepts. Things like lines and shapes (triangles, squares, circles etc.). Not only do we understand these concepts, we can also combine them in a infinite, recursive way to form new geometrical forms. We can also transform them through rotation. This is important for chess. Chess relies on geometrical concepts fundamentally. The concept of a line of varying discrete lengths (a line distance of 1 for a pawn, 2 on the first move). A vertical line rotated by 45 degrees for the length of a bishop. A knight is an example of a recursive transformation, combining 1 and 2 length lines at 90 degree angles. Same with the queen (diagonal and straight). Numerosity is also fundamental. The piece involves an understanding of numerosity to move a certain amount of squares.

This may seem obvious, but it needs to pointed out because everyday experience disguises the miracle. These geometrical concepts do not exist in nature. There are no lines and squares. If it's obvious then why did it take 4.5 billion years since the development of life to emerge?

Animals do not possess a sense of discrete numbers.

Animals do not possess a sense of discrete numbers. Chimpanzees, instead of seeing 6 and 7, they feel 6ish-7ish. This is shown when they have to pick a plate with the most food. The further the difference between the amount of chocolate chips, the easier it is for them (e.g. choosing between 2 and 10 chocolate chips). They get it right when it's between 1 and 2 chocolate chips. But if it's between 6 and 7, then it's difficult, the performance decreases when the ratio between the amount of chips decreases. This is represented by Weber's Law which states that the threshold needed to detect a stimulus grows in proportion with the initial stimulus (e.g. to have an equal performance for comparing 1 vs 2 chips might have to have an equivalent of 6 vs 12 chips as an example). Without a sense of discrete numbers, you can't play chess.

There was a study where they had bonobos try to pick out the odd shape out.

There was a study where they had bonobos try to pick out the odd shape out. So there were a bunch of squares and there was an irregular quadrilateral (four sided polygon). Humans found it easier to spot the odd shape out when the shape was a regular square against a background of irregular quadrilaterals and vice versa (image shown below). When the odd shape out was a irregular quadrilateral amongst other irregular quadrilaterals, humans found it harder. But bonobos didn't have any effect like this, and whether the squares were there or not didn't affect the ease of the task (they did equally poorly either way with a much worse performance than humans). This shows how humans have a specific ability to understand geometric shapes.

Image 1. Find the shape that is not a regular square. Image 2. Find the shape that is a regular square. Sablé‐Meyer et al. (2024) Two brain systems for the perception of geometric shapes

Where squares were involved or not as an odd object out, baboons made the same amount of errors (75% of first trials improving to 50% on later trials, but this patterns was the same not matter where the shape to be detected was a regular square or a not a regular geometric shape). Humans only made 0-10% errors on regular geometric shapes, increasing to 40% on shapes that were non-regular. Dehaene et al. (2022) Symbols and mental programs: a hypothesis about human singularity

Understanding regular shapes means we can create a 8x8 chess board through squares. This involves the concept symmetry/repetition.

Shapes are hypothesized to be formed by a Minimum Description Length program.

Shapes are hypothesized to be formed by a Minimum Description Length program. The brain finds the most efficient way to encode a shape using a program which describes the shape. This compresses the description of the shape to its minimum length. Human memory performance on shape based tasks have been shown to match the concept of Minimum Description Length quite well. Memory performance of zigzag patterns varies with the Minimum Description Length which views the zigzag sequence in chunks.

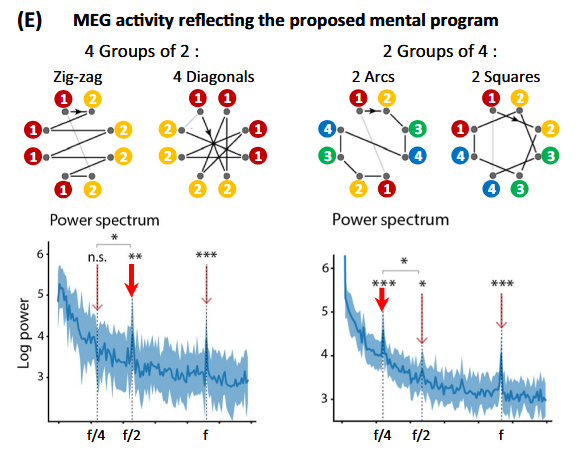The zigzag patterns are converted to geometrical regularities with the use of symmetry and repetition. Brain activity supports this view as measured using Magnetoencephalography (MEG), which measures magnetic fields causes by electrical activity in the brain. Dehaene et al. (2022) Symbols and mental programs: a hypothesis about human singularity

Minimum Length Description explains the paradox of why circles are viewed as a simple shape. Technically circles are the most complicated as they have infinite sides. But circles are easier to conceptualize then a 17-sided polygon for example, even though a circle has infinite sides. The Minimum Length Description gives an answer to this. The answer is that a circle only needs one angle rate parameter: a circle is formed by a single line with a constant rate of rotation from one of its endpoints. Now the description switches from amount of sides to a single angle sweep rate parameter.

Being able to represent complex geometrical sequences allows us to create the movements which guide the chess pieces. It also allows us to memorize opening theory and chess games. If you think about it, thinking about chess moves is incredibly complicated, involving memorizing or visualizing long sequences of geometrical patterns. You don't notice this because it feels normal and the piece visuals make it seem like the moves emanate from them naturally.

Everyday experience disguises the miracle.

Sources

Stanislas Dehaene (1997). The Number Sense
Dehaene et al. (2022). Symbols and mental programs: a hypothesis about human singularity
Sablé‐Meyer et al. (2024). A language of thought for the mental representation of geometrical shapes
Sablé‐Meyer et al. (2024). Two brain systems for the perception of geometric shapes

---
Visit Blog Creators Hangout for more featured blogs.